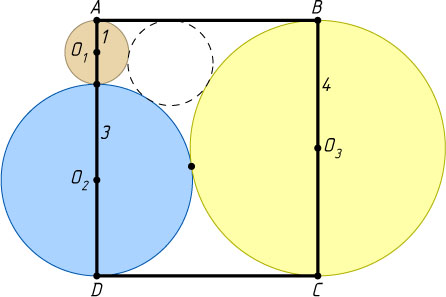
2982. Центры окружностей с радиусами 1, 3 и 4 расположены на сторонах AD
и BC
прямоугольника ABCD
. Эти окружности касаются друг друга и прямых AB
и CD
так, как показано на рисунке. Докажите, что существует окружность, касающаяся всех этих окружностей и прямой AB
.
Указание. Пусть S_{1}
, S_{2}
, S_{3}
окружности радиусов 1, 3, 4 соответственно, Достаточно доказать, что — радиус окружности, касающейся окружностей S_{1}
, S_{2}
и луча AB
равен радиусу окружности, касающейся окружностей S_{2}
, S_{3}
и луча BA
.
Решение. Пусть O_{1}
, O_{2}
, O_{3}
— центры окружностей S_{1}
, S_{2}
, S_{3}
радиусов 1, 3, 4 соответственно, x
— радиус окружности S
с центром O
, касающейся окружностей S_{1}
, S_{2}
и луча AB
, y
— радиус окружности S'
с центром O'
, касающейся окружностей S_{2}
, S_{3}
и луча BA
.
Достаточно доказать, что x=y
, так как при данном в условии задачи расположении окружностей существует единственная окружность данного радиуса, касающаяся данного луча и данной окружности.
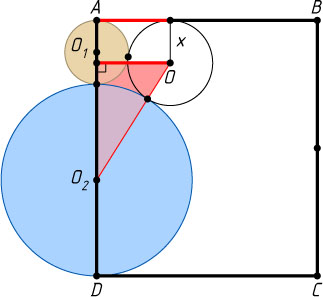
Расстояние от точки O
до прямой AD
равно длине отрезка общей внешней касательной окружностей S
и S_{1}
(рис. 1), т. е. 2\sqrt{1\cdot x}=2\sqrt{x}
(см. задачу 365). С другой стороны, это расстояние равно катету прямоугольного треугольника с гипотенузой OO_{2}=3+x
и катетом, равным AD-x-3=5-x
. Из уравнения
(3+x)^{2}-(5-x)^{2}=4x
находим, что x=\frac{4}{3}
.
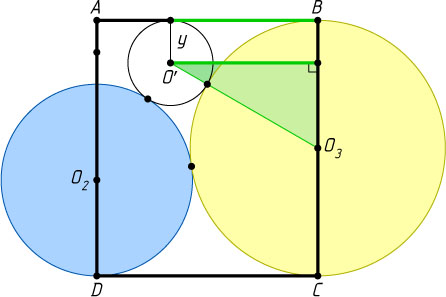
Сторона CD
— общая касательная к касающимся окружностям S_{1}
и S_{3}
(рис. 2), поэтому CD=2\sqrt{3\cdot4}=4\sqrt{3}
. Расстояние от точки O'
до прямой BC
равно длине отрезка общей внешней касательной окружностей S'
и S_{3}
, т. е. 4\sqrt{y}
. Тогда расстояние от точки O'
до прямой AD
равно CD-4\sqrt{y}=4\sqrt{3}-4\sqrt{y}
.
С другой стороны, это расстояние равно катету прямоугольного треугольника с гипотенузой O'O_{3}=3+y
и катетом, равным AD-y-3=5-y
. Из уравнения
(3+y)^{2}-(5-y)^{2}=(4\sqrt{3}-4\sqrt{y})^{2}
находим, что y=\frac{4}{3}=x
. Что и требовалось доказать.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 12.67, с. 307
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 12.69, с. 294


