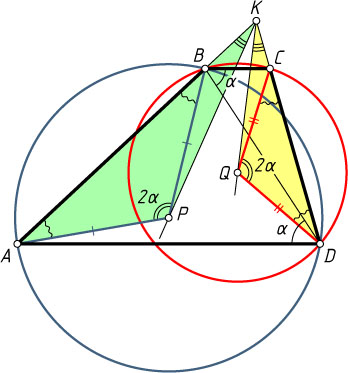
2992. В трапеции ABCD
с основаниями AD
и BC
лучи AB
и DC
пересекаются в точке K
. Точки P
и Q
— центры описанных окружностей треугольников ABD
и BCD
. Докажите, что \angle PKA=\angle QKD
.
Указание. Докажите подобие треугольников APK
и KQD
.
Решение. Заметим, что \angle ADB=\angle DBC
как внутренние накрест лежащие при параллельных прямых AD
и BC
и секущей BD
. С другой стороны, \angle APB=2\angle ADB
, поскольку в окружности, описанной около треугольника ABD
, угол ADB
вписанный, а угол APB
центральный. Аналогично получим, что \angle DQC=2\angle DBC
, а значит,
\angle APB=2\angle ADB=2\angle DBC=\angle DQC.
Далее, поскольку AP=PB
и DQ=QC
, треугольники APB
и DQC
подобны по двум сторонам и углу между ними. Поэтому \angle KAP=\angle KDQ
и AP:DQ=AB:DC
. Вместе с тем из теоремы о пропорциональных отрезках AK:DK=AB:DC
, поэтому треугольники APK
и DQK
подобны по двум сторонам и углу между ними. Отсюда следует, что \angle PKA=\angle QKD
.
Автор: Акопян А. В.
Источник: Московская математическая олимпиада. — 2011, LXXIV, 9 класс
