2993. В треугольнике ABC
проведены биссектрисы BB_{1}
и CC_{1}
. Известно, что центр описанной окружности треугольника BB_{1}C_{1}
лежит на прямой AC
. Найдите угол C
треугольника.
Ответ. 120^{\circ}
.
Указание. Точка, симметричная C_{1}
относительно прямой AC
, лежит на описанной окружности треугольника BB_{1}C_{1}
Решение. Продолжив луч BC
до пересечения с описанной окружностью треугольника BB_{1}C_{1}
, получим точку K
. Вписанные углы \angle C_{1}BB_{1}
и \angle KBB_{1}
равны (так как BB_{1}
— биссектриса), значит, равны дуги, на которые они опираются, \smile B_{1}C_{1}=\smile B_{1}K
. При этом точки K
и C_{1}
лежат на окружности (описанной вокруг треугольника BB_{1}C_{1}
), центр которой принадлежит прямой AC
. Следовательно, K
и C_{1}
симметричны друг другу относительно прямой AC
. Получаем равенство трёх углов
\angle BCC_{1}=\angle C_{1}CB_{1}=\angle B_{1}CK.
Сумма этих углов равна 180^{\circ}
, значит, каждый из них равен 60^{\circ}
. Следовательно,
\angle ACB=\angle BCC_{1}+\angle C_{1}CB_{1}=120^{\circ}.
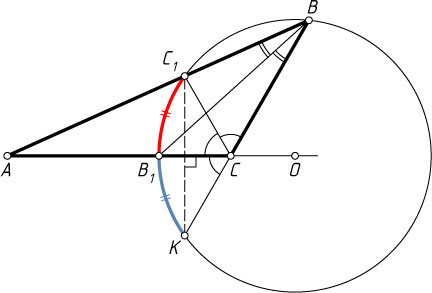
Примечание. 1. Легко показать, что центр O
окружности может лежать только на продолжении отрезка AC
за точку C
и, значит, прямая BC
пересекает окружность именно так, как показано на рисунке.
2. Возможны также решения, основанные на том, что точки B
, C
, O
, C_{1}
лежат на одной окружности, или на том, что описанная окружность треугольника BC_{1}B_{1}
является окружностью Аполлония для точек A
и C
.
Автор: Заславский А. А.
Источник: Московская математическая олимпиада. — 2011, LXXIV, 10 класс
