2996. Внутри треугольника ABC
взята такая точка O
, что \angle ABO=\angle CAO
, \angle BAO=\angle BCO
, \angle BOC=90^{\circ}
. Найдите отношение AC:OC
.
Ответ. \sqrt{2}
.
Указание. Пусть D
— точка, симметричная точке C
относительно прямой OB
. Тогда точки A
, O
, B
и D
лежат на одной окружности, а треугольники DAC
и AOC
подобны по двум углам.
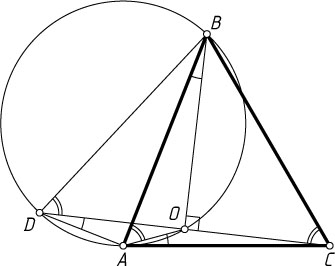
Решение. Первый способ. Построим точку D
, симметричную точке C
относительно прямой BO
(рис. 1). Тогда \angle BDO=\angle BCO=\angle BAO
. Значит, точка D
лежит на окружности, описанной около треугольника ABO
. По теореме о вписанных углах
\angle ADO=\angle ABO=\angle CAO,
поэтому треугольник DAC
подобен треугольнику AOC
по двум углам (угол при вершине C
— общий). Следовательно, \frac{DC}{AC}=\frac{AC}{OC}
, или \frac{2OC}{AC}=\frac{AC}{OC}
, откуда находим, что \frac{AC}{OC}=\sqrt{2}
.
Второй способ. Поскольку \angle BAO=\angle BCO
, точки A
и C
принадлежат ГМТ, из которых отрезок BO
виден под одним углом (рис. 2). Это ГМТ состоит их двух дуг окружностей (без точек B
и O
), расположенных по разные стороны от прямой BO
.
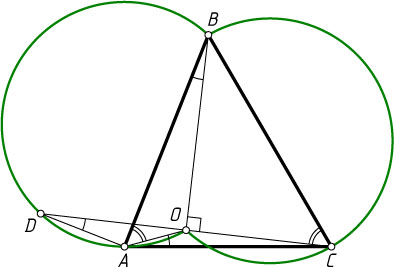
Пусть прямая CO
пересекает содержащую точку A
дугу ГМТ в точке D
(точка O
лежит между точками D
и C
). Так как угол BOC
прямой, то \angle DOB=\angle COB
и DO=OC
. При этом \angle ODA=\angle OBA
как вписанные углы, опирающиеся на одну и ту же дугу, и \angle OBA=\angle OAC
по условию. Поэтому треугольник AOC
подобен треугольнику DAC
по двум углам. Значит, \frac{OC}{AC}=\frac{AC}{CD}=\frac{AC}{2OC}
. Следовательно, \frac{AC}{OC}=\sqrt{2}
.
Примечание. Отметим, что у этой задачи есть и другие решения, в которых используются теорема Чевы для треугольника ABC
и теорема синусов для треугольников AOB
, AOC
и BOC
.
Автор: Сергеев И. Н.
Источник: Московская математическая олимпиада. — 2011, LXXIV, 11 класс

