2999. Окружность \omega
, вписанная в остроугольный неравнобедренный треугольник ABC
, касается стороны BC
в точке D
. Пусть точка I
— центр окружности \omega
, а O
— центр окружности, описанной около треугольника ABC
. Окружность, описанная около треугольника AID
, пересекает вторично прямую AO
в точке E
. Докажите, что длина отрезка AE
равна радиусу окружности \omega
.
Решение. Обозначим \angle BAC=\alpha
, \angle ACB=\gamma
, r
— радиус вписанной окружности треугольника ABC
. Тогда \angle AOB=2\gamma
(центральный угол вдвое больше вписанного), \angle CAI=\angle BAI=\frac{\alpha}{2}
(AI
— биссектриса угла BAC
) и \angle BAO=90^{\circ}-\gamma
как угол при основании равнобедренного треугольника AOB
.
Пусть прямая ID
пересекает OA
и AC
в точках P
и Q
соответственно. По теореме о внешнем угле треугольника
\angle AIP=\angle AIQ=\angle CQD-\angle IAQ=90^{\circ}-\gamma-\frac{\alpha}{2}.
С другой стороны,
\angle PAI=\angle OAB-\angle BAI=90^{\circ}-\gamma-\frac{\alpha}{2},
значит, \angle AIP=\angle PAI
. Следовательно, PA=PI
.
Из равенств PA=PI
и PA\cdot PE=PI\cdot PD
следует, что PE=PD
, поэтому
AE=PE-PA=PD-PI=ID=r.
Что и требовалось доказать.
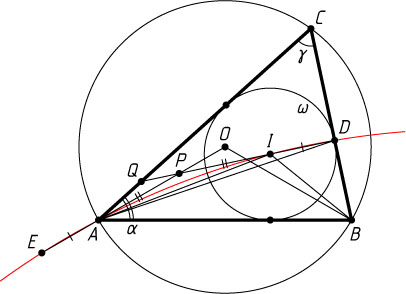
Автор: Емельянов Л. А.
Источник: Всероссийская олимпиада школьников. — 2011-12, XXXVIII, заключительный этап, 10 класс
Источник: Журнал «Квант». — 2012, № 5-6, с. 62
