3004. Данный параллелограмм разделите на три равновеликие части прямыми, выходящими из одной вершины.
Указание. Сведите задачу к проведению через вершину треугольника прямой, делящей его площадь в отношении 2:1
.
Решение. Пусть A
— данная вершина параллелограмма ABCD
. Построим точки M
и N
на сторонах соответственно BC
и DC
так, чтобы
\frac{BM}{MC}=\frac{DN}{NC}=2.
Пусть S
— площадь параллелограмма ABCD
. Тогда
S_{\triangle ABM}=\frac{2}{3}S_{\triangle ABC}=\frac{2}{3}\cdot\frac{1}{2}S=\frac{1}{3}S,
S_{\triangle ADN}=\frac{2}{3}S_{\triangle ADC}=\frac{2}{3}\cdot\frac{1}{2}S=\frac{1}{3}S.
Поэтому
S_{AMCN}=S-S_{\triangle ABM}-S_{\triangle ADN}=S-\frac{1}{3}S-\frac{1}{3}S=\frac{1}{3}S.
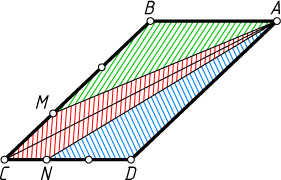
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. —
