3006. На стороне AB
треугольника ABC
взяты точки M
и N
, причём AM:MN:NB=2:2:1
, а на стороне AC
— точка K
, причём AK:KC=1:2
. Найдите площадь треугольника MNK
, если площадь треугольника ABC
равна 1.
Ответ. \frac{2}{15}
.
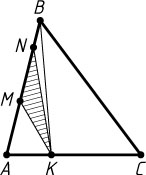
Указание. Проведите BK
.
Решение. Соединим K
и B
. Тогда
S_{\triangle AKB}=\frac{1}{3}S_{\triangle ABC},~S_{\triangle MNK}=\frac{2}{5}S_{\triangle AKB}.
Поэтому
S_{\triangle MNK}=\frac{2}{5}\cdot\frac{1}{3}S_{\triangle ABC}=\frac{2}{15}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 7.3, с. 52
