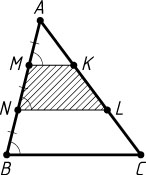
3009. Через точки M
и N
, делящие сторону AB
треугольника ABC
на три равные части, проведены прямые, параллельные стороне BC
. Найдите площадь части треугольника, заключённой между этими прямыми, если площадь треугольника ABC
равна 1.
Ответ. \frac{1}{3}
.
Указание. Площади подобных треугольников относятся, как квадраты соответствующих сторон.
Решение. Пусть AM=MN=NB
, точки K
и L
лежат на стороне AC
и MK\parallel NL\parallel BC
. Тогда треугольник AMK
подобен треугольнику ABC
с коэффициентом \frac{1}{3}
, а треугольник ANL
подобен треугольнику ABC
с коэффициентом \frac{2}{3}
, следовательно,
S_{MKLN}=S_{\triangle ANL}-S_{\triangle AMK}=\frac{4}{9}S_{\triangle ABC}-\frac{1}{9}S_{\triangle ABC}=\frac{1}{3}S_{\triangle ABC}=\frac{1}{3}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 7.4, с. 52
