3011. На сторонах AB
и AD
параллелограмма ABCD
взяты точки M
и N
так, что прямые MC
и NC
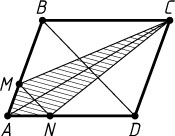
разбивают параллелограмм на три равновеликие части. Найдите MN
, если BD=d
.
Ответ. \frac{1}{3}d
.
Указание. Найдите отношения, в которых точки M
и N
делят стороны AB
и AD
.
Решение. Поскольку
S_{\triangle ABC}=S_{\triangle CDA},~S_{\triangle MBC}=\frac{2}{3}S_{\triangle ABC},
то \frac{AM}{MB}=\frac{1}{2}
. Аналогично \frac{AN}{ND}=\frac{1}{2}
. Следовательно, треугольник AMN
подобен треугольнику ABD
с коэффициентом \frac{AM}{AB}=\frac{1}{3}
. Поэтому
MN=\frac{1}{3}BD=\frac{1}{3}d.
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 54, с. 11
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 54, с. 9
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 7.21, с. 54
