3014. В равнобедренном треугольнике ABC
боковые стороны BC
и AC
в два раза больше основания AB
. Биссектрисы углов при основании пересекаются в точке M
. Какую часть треугольника ABC
составляет площадь треугольника AMB
?
Ответ. \frac{1}{5}
.
Указание. Биссектриса делит основание треугольника на отрезки, пропорциональные боковым сторонам.
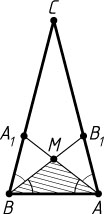
Решение. Пусть AA_{1}
и BB_{1}
— биссектрисы углов при основании AB
треугольника ABC
. Поскольку
\frac{BA_{1}}{A_{1}C}=\frac{AB}{AC}=\frac{1}{2},~BA_{1}=\frac{1}{3}BC,
то
S_{\triangle ABA_{1}}=\frac{1}{3}S_{\triangle ABC}.
Поскольку BM
— биссектриса треугольника BAA_{1}
, то
\frac{A_{1}M}{AM}=\frac{BA_{1}}{AB}=\frac{2}{3},~AM=\frac{3}{5}AA_{1}.
Следовательно,
S_{\triangle AMB}=\frac{3}{5}S_{\triangle ABA_{1}}=\frac{1}{5}S_{\triangle ABC}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 7.18, с. 53
