3015. Из середины основания треугольника проведены прямые, параллельные боковым сторонам. Докажите, что площадь полученного таким образом параллелограмма равна половине площади треугольника.
Указание. Площадь параллелограмма равна произведению его соседних сторон на синус угла между ними.
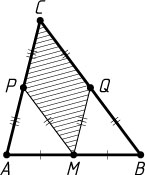
Решение. Пусть M
— середина основания AB
треугольника ABC
; P
и Q
— вершины параллелограмма MPCQ
, принадлежащие сторонам AC
и BC
. Тогда P
и Q
— середины сторон AC
и BC
. Следовательно,
S_{MPCQ}=CQ\cdot CP\sin\angle C=\frac{1}{2}BC\cdot\frac{1}{2}AC\sin\angle C=\frac{1}{2}S_{\triangle ABC}.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 47, с. 81
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 7.7, с. 52
