3016. Докажите, что если какую-либо точку внутри параллелограмма соединить со всеми его вершинами, то сумма площадей двух противолежащих треугольников равна сумме площадей двух других.
Указание. Докажите, что сумма площадей двух противоположных треугольников равна половине площади параллелограмма (или проведите через данную точку прямые, параллельные сторонам параллелограмма).
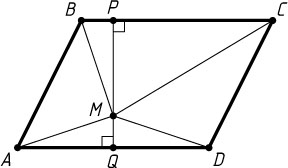
Решение. Первый способ. Пусть M
— точка внутри параллелограмма ABCD
, P
и Q
— её проекции на прямые BC
и AD
. Тогда
S_{\triangle MBC}+S_{\triangle AMD}=\frac{1}{2}BC\cdot MP+\frac{1}{2}AD\cdot MQ=
=\frac{1}{2}AD\cdot(MP+MQ)=\frac{1}{2}AD\cdot PQ,
причём PQ
— высота параллелограмма ABCD
. Поэтому найденная сумма равна половине площади параллелограмма.
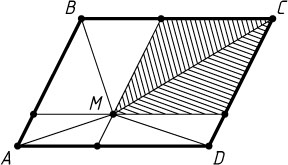
Второй способ. Через точку M
, взятую внутри параллелограмма ABCD
, проведём прямые, параллельные сторонам параллелограмма. Эти прямые разбивают параллелограмм на четыре меньших параллелограмма. Диагонали AM
, BM
, CM
и DM
разбивают каждый из этих четырёх параллелограммов на два равных треугольника. Отсюда следует утверждение задачи.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — № 296(1), с. 232
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 48, с. 81
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 4, с. 81

