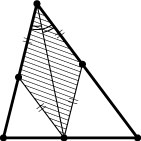
3024. Треугольник и вписанный в него ромб имеют общий угол. Стороны треугольника, заключающие этот угол, относятся как \frac{m}{n}
. Найдите отношение площади ромба к площади треугольника.
Ответ. \frac{2mn}{(m+n)^{2}}
.
Указание. Стороны ромба отсекают от треугольника подобные ему треугольники с коэффициентами подобия, равными \frac{n}{m+n}
и \frac{m}{m+n}
.
Решение. Диагональ ромба, проведённая из общей с треугольником вершины, является биссектрисой треугольника. Поэтому она делит сторону в отношении \frac{m}{n}
.
Стороны ромба отсекают от треугольника подобные ему треугольники с коэффициентами подобия \frac{n}{m+n}
и \frac{m}{m+n}
. Поэтому их площади равны \frac{n^{2}}{(m+n)^{2}}\cdot S
и \frac{m^{2}}{(m+n)^{2}}\cdot S
, где S
— площадь данного треугольника. Значит, площадь ромба равна
S-\frac{n^{2}}{(m+n)^{2}}\cdot S-\frac{m^{2}}{(m+n)^{2}}\cdot S=\frac{2mn}{(m+n)^{2}}\cdot S.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 143, с. 92
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 7.10, с. 53
