3026. Две прямые, параллельные основаниям трапеции, делят каждую из боковых сторон на три равные части. Вся трапеция разделена ими на три части. Найдите площадь средней части, если площади крайних равны S_{1}
и S_{2}
.
Ответ. \frac{S_{1}+S_{2}}{2}
.
Указание. Через вершину меньшего основания проведите прямую, параллельную боковой стороне трапеции.
Решение. Пусть MN
и KL
— указанные прямые, параллельные основаниям AD
и BC
трапеции ABCD
(M
и K
на AB
, N
и L
на CD
); прямая, проходящая через вершину C
меньшего основания параллельно боковой стороне AB
, пересекает MN
, KL
и AD
в точках P
, Q
и R
соответственно.
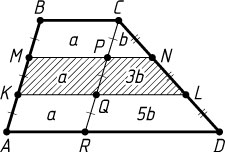
Обозначим площади равных параллелограммов MBCP
, KMPQ
и AKQR
через a
, а площадь треугольника CPN
через b
. Тогда
S_{QPNL}=4b-b=3b,~S_{RQLD}=9b-4b=5b,
S_{1}=S_{MBCN}=a+b,~S_{2}=S_{AKLD}=a+5b.
Следовательно,
S_{3}=S_{KMNL}=a+3b=\frac{2a+6b}{2}=\frac{S_{1}+S_{2}}{2}.
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 38, с. 10
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 38, с. 8
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 7.11, с. 53
