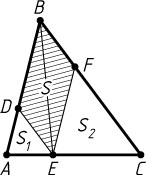
3029. На стороне AC
треугольника ABC
взята точка E
. Через точку E
проведена прямая DE
параллельно стороне BC
и прямая EF
параллельно стороне AB
(D
и F
— точки на сторонах треугольника). Докажите, что S_{BDEF}=2\sqrt{S_{\triangle ADE}\cdot S_{\triangle EFC}}
.
Указание. Коэффициент подобия треугольников ADE
и EFC
равен \sqrt{\frac{S_{\triangle ADE}}{S_{\triangle EFC}}}
.
Решение. Поскольку
\frac{1}{2}\cdot\frac{S_{BDEF}}{S_{\triangle ADE}}=\frac{S_{\triangle BDE}}{S_{\triangle ADE}}=\frac{DB}{AD}=\frac{EF}{AD}=\sqrt{\frac{S_{\triangle EFC}}{S_{\triangle ADE}}},
то
S_{BDEF}=2\sqrt{S_{\triangle ADE}\cdot S_{\triangle EFC}}.
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 47, с. 140
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 1.34, с. 15
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 7.8, с. 52
