3031. В параллелограмме соединены середина каждой стороны с концом следующей стороны, отчего получился внутренний параллелограмм. Докажите, что его площадь составляет \frac{1}{5}
площади данного параллелограмма.
Решение. Пусть K
, L
, M
и N
— середины сторон соответственно AB
, BC
, CD
и AD
параллелограмма ABCD
, площадь которого равна S
. Площадь параллелограмма, образованного пересечениями прямых AL
, BM
, CN
и DK
, обозначим через s
.
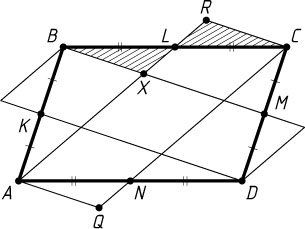
Через вершины A
и C
проведём прямые, параллельные BM
. Точки пересечения этих прямых с прямыми AL
и CN
являются вершинами параллелограмма ARCQ
(точки C
и R
лежат по одну сторону от прямой BM
).
Аналогично построим параллелограмм с противоположными вершинами B
и D
. Общая часть двух построенных параллелограммов есть внутренний параллелограмм, о котором говорится в условии задачи.
Если X
— точка пересечения прямых AR
и BM
, то треугольник LRC
равен треугольнику LXB
по стороне и двум прилежащим к ней углам. Аналогично для всех таких треугольников, расположенных вне исходного параллелограмма.
Тогда площадь «креста», образованного двумя построенными параллелограммами, равна площади исходного параллелограмма, т. е. S
. В то же время, «крест» состоит из пяти равных параллелограммов, один из которых — параллелограмм, площадь s
которого нужно найти. Следовательно,
s=\frac{1}{5}S.
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 29, с. 138
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 133, с. 91
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 1, с. 178
Источник: Устный вступительный экзамен в МФТИ. — 1953, № 3, билет 3
Источник: Задачи по математике и физике, дававшиеся на приёмных испытаниях в 1947—1953 гг. — М.: МФТИ, 1956. — № 3, с. 8
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 335, с. 39
