3033. Площадь треугольника ABC
равна S
. Найдите площадь треугольника, стороны которого равны медианам треугольника ABC
.
Ответ. \frac{3}{4}S
.
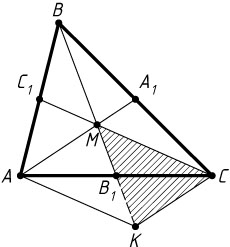
Указание. Пусть M
— точка пересечения медиан треугольника ABC
. Достройте треугольник AMC
до параллелограмма AMCK
и рассмотрите треугольник MCK
.
Решение. Пусть M
— точка пересечения медиан треугольника ABC
, B_{1}
— середина стороны AC
.
Отложим на продолжении медианы BB_{1}
за точку B_{1}
отрезок B_{1}K
, равный B_{1}M
. Поскольку AMCK
— параллелограмм, то KC=AM
. Поэтому стороны треугольника MCK
равны \frac{2}{3}
сторон треугольника, составленного из медиан треугольника ABC
.
Следовательно, искомый треугольник подобен треугольнику MCK
с коэффициентом \frac{3}{2}
, а его площадь равна \frac{9}{4}
площади треугольника MCK
, т. е.
\frac{9}{4}\cdot2\cdot\frac{1}{6}S=\frac{3}{4}S.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.320, с. 180
Источник: Факультативный курс по математике: Учебное пособие для 7—9 кл. средней школы / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — с. 92
Источник: Вступительный экзамен в МФТИ. — 1954, билет 10, № 1
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 54-10-1, с. 47
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 27, с. 39
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 324, с. 38
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 15
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 1.37, с. 15
