3034. Трапеция ABCD
разделена прямой, параллельной её основаниям AD
и BC
, на две равновеликие трапеции. Найдите отрезок этой прямой, заключённый между боковыми сторонами, если основания трапеции равны a
и b
.
Ответ. \sqrt{\frac{a^{2}+b^{2}}{2}}
.
Указание. С помощью дополнительных построений получите подобные треугольники.
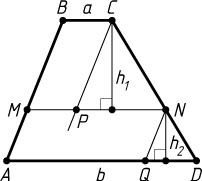
Решение. Первый способ. Пусть точки M
и N
расположены на боковых сторонах AB
и CD
трапеции ABCD
, P
— точка пересечения с MN
прямой, проходящей через точку C
параллельно AB
, Q
— точка пересечения с AD
прямой, проходящей через точку N
параллельно AB
. Обозначим MN=x
; h_{1}
и h_{2}
— высоты подобных треугольников PCN
и QND
(рис. 1).
Пусть BC=a
и AD=b
(b\gt a
). Из равенства площадей трапеций BMNC
и MADN
следует, что
(x+a)h_{1}=(b+x)h_{2},
откуда \frac{h_{1}}{h_{2}}=\frac{b+x}{x+a}
.
Из подобия треугольников CPN
и NQD
следует, что \frac{h_{1}}{h_{2}}=\frac{x-a}{b-x}
. Поэтому
\frac{b+x}{x+a}=\frac{x-a}{b-x}.
Из этого уравнения находим, что x=\sqrt{\frac{a^{2}+b^{2}}{2}}
.
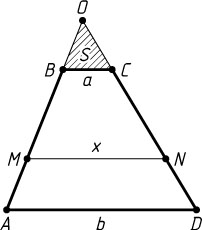
Второй способ. Пусть O
— точка пересечения продолжений боковых сторон AB
и DC
(рис. 2), S
— площадь треугольника BOC
, MN=x
— искомый отрезок. Тогда S_{\triangle MNO}-S=S_{\triangle AOD}-S_{\triangle MNO}
, или
\frac{x^{2}}{a^{2}}\cdot S-S=\frac{b^{2}}{a^{2}}\cdot S-\frac{x^{2}}{a^{2}}\cdot S.
Отсюда находим, что x^{2}=\frac{a^{2}+b^{2}}{2}
.
Источник: Вступительный экзамен в МФТИ. — 1962, билет 2, № 2
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 62-2-2, с. 90
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 10, с. 178
Источник: Шарыгин И. Ф. Геометрия 7—9: Учебник для общеобразовательных учебных заведений. — М.: Дрофа, 2002. — № 21, с. 262
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.318, с. 180
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.30, с. 32
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 115(а), с. 21
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 1.35, с. 15

