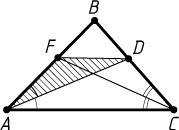
3035. В треугольнике ABC
проведены биссектрисы CF
и AD
. Найдите отношение площадей треугольников AFD
и ABC
, если AB:AC:BC=21:28:20
.
Ответ. \frac{1}{4}
.
Указание. Воспользуйтесь свойством биссектрисы треугольника.
Решение. По свойству биссектрисы треугольника
\frac{BD}{DC}=\frac{AB}{AC}=\frac{21}{28}=\frac{3}{4}.
Поэтому S_{\triangle ABD}=\frac{3}{7}S_{\triangle ABC}
, а так как
\frac{AF}{FB}=\frac{AC}{CB}=\frac{28}{20}=\frac{7}{5},
то
S_{\triangle AFD}=\frac{7}{12}S_{\triangle ABD}=\frac{7}{12}\cdot\frac{3}{7}S_{\triangle ABC}=\frac{3}{12}S_{\triangle ABC}=\frac{1}{4}S_{\triangle ABC}.
Источник: Вступительный экзамен на геологический факультет МГУ. — вариант 1, № 2
Источник: Моденов П. С. Экзаменационные задачи по математике с анализом их решения. — М.: Просвещение, 1969. — вариант 1, № 2, с. 331
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 7.9, с. 52
