3044. Площадь трапеции ABCD
равна 30. Точка P
— середина боковой стороны AB
. Точка R
на стороне CD
выбрана так, что 2CD=3RD
. Прямые AR
и PD
пересекаются в точке Q
. Найдите площадь треугольника APQ
, если AD=2BC
.
Ответ. \frac{10}{3}
.
Указание. Найдите отношение \frac{PQ}{QD}
.
Решение. Пусть BC=a
, AD=2a
; h
— высота данной трапеции. Тогда
S_{ABCD}=\frac{AD+BC}{2}\cdot h=\frac{3}{2}ah=30.
Отсюда находим, что ah=20
.
Пусть T
— точка пересечения прямых AR
и BC
. Из подобия треугольников CRT
и DRA
находим, что
CT=\frac{DR}{RC}\cdot AD=\frac{1}{2}AD=a.
Поэтому BT=AD
, а ABTD
— параллелограмм.
Из подобия треугольников APQ
и TDQ
находим, что
\frac{PQ}{QD}=\frac{AP}{TD}=\frac{AP}{AB}=\frac{1}{2}.
Следовательно,
S_{\triangle APQ}=\frac{1}{3}S_{\triangle APD}=\frac{1}{3}\cdot\frac{1}{2}\cdot AD\cdot\frac{h}{2}=
=\frac{1}{12}AD\cdot h=\frac{1}{6}ah=\frac{1}{6}\cdot20=\frac{10}{3}.
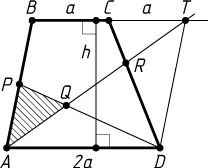
Источник: Вступительный экзамен на биологический факультет МГУ. — 1987, вариант 1, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 76
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 7.14, с. 53
