3047. Пусть M
, N
, K
и L
— середины сторон CD
, DA
, AB
и BC
квадрата ABCD
, площадь которого равна S
. Найдите площадь четырёхугольника, образованного прямыми AM
, BN
, CK
и DL
.
Ответ. \frac{1}{5}S
.
Указание. Найдите отношение отрезков, на которые отрезок BN
делится отрезками AM
и CK
.
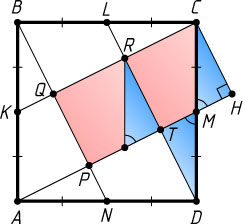
Решение. Пусть прямые AM
и BN
пересекаются в точке P
, BN
и CK
— в точке Q
, CK
и DL
— в точке R
, DL
и AM
— в точке T
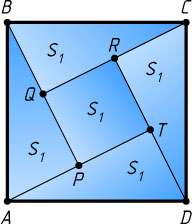
(рис. 1). Тогда PQRT
— также квадрат. Опустим перпендикуляр CH
из вершины C
исходного квадрата на прямую AM
. Заметим, что RCHT
— квадрат, равный квадрату PQRT
. Поскольку треугольники CHM
и DTM
равны, то они равновелики. Значит, площадь квадрата RCHT
равна площади треугольника DCR
. Рассуждая аналогично, придём к тому, что площадь квадрата ABCD
равна пяти площадям квадрата PQRT
(рис. 2).
