3051. Из точки P
, расположенной внутри остроугольного треугольника ABC
, опущены перпендикуляры на его стороны. Длины сторон и опущенных на них перпендикуляров соответственно равны a
и k
, b
и m
, c
и n
. Найдите отношение площади треугольника ABC
к площади треугольника, вершинами которого служат основания перпендикуляров.
Ответ. \frac{abc}{kmc+nma+knb}
.
Указание. Синусы углов между указанными перпендикулярами равны синусам соответствующих углов треугольника ABC
.
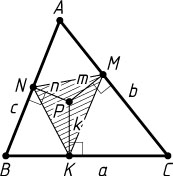
Решение. Пусть K
, M
и N
— основания перпендикуляров, опущенных из точки P
на стороны BC=a
, AC=b
, AB=c
соответственно; PK=k
, PM=m
, PN=n
. Тогда
S_{\triangle KMN}=S_{\triangle MPN}+S_{\triangle KPN}+S_{\triangle MPK}=
=\frac{1}{2}mn\sin(180^{\circ}-\angle A)+\frac{1}{2}kn\sin(180^{\circ}-\angle B)+\frac{1}{2}km\sin(180^{\circ}-\angle C)=
=\frac{1}{2}(mn\sin\angle A+kn\sin\angle B+km\sin\angle C).
Следовательно,
\frac{S_{\triangle KMN}}{S_{\triangle ABC}}=\frac{\frac{1}{2}(mn\sin\angle A+kn\sin\angle B+km\sin\angle C)}{\frac{1}{2}bc\sin\angle A}=
=\frac{mn+kn\cdot\frac{\sin\angle B}{\sin\angle A}+km\cdot\frac{\sin\angle C}{\sin\angle A}}{bc}=\frac{mn+kn\cdot\frac{b}{a}+km\cdot\frac{c}{a}}{bc}=\frac{nma+knb+kmc}{abc}.
Источник: Вступительный экзамен на химический факультет МГУ. — 1979, вариант 1, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 42
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 7.27, с. 54
