3052. Из точки P
, расположенной внутри остроугольного треугольника ABC
, опущены перпендикуляры на стороны AB
, BC
и CA
. Перпендикуляры соответственно равны l
, m
, n
. Вычислите площадь треугольника ABC
, если углы BAC
, ABC
и ACB
соответственно равны \alpha
, \beta
и \gamma
.
Ответ. \frac{(l\sin\gamma+m\sin\alpha+n\sin\beta)^{2}}{2\sin\alpha\sin\beta\sin\gamma}
.
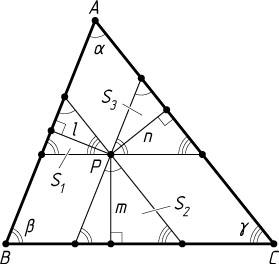
Указание. Проведите через точку P
прямые, параллельные сторонам треугольника. Они разбивают треугольник ABC
на 6 частей, три из которых — треугольники. Если их площади S_{1}
, S_{2}
, S_{3}
, то S_{\triangle ABC}=(\sqrt{S_{1}}+\sqrt{S_{2}}+\sqrt{S_{3}})^{2}
.
Решение. Проведём через точку P
прямые, параллельные сторонам треугольника ABC
. Они разобьют треугольник ABC
на шесть частей, три из которых — треугольники с углами \alpha
, \beta
, \gamma
и высотами l
, m
, n
. Если площади этих треугольников равны соответственно S_{1}
, S_{2}
и S_{3}
, то
S_{\triangle ABC}=(\sqrt{S_{1}}+\sqrt{S_{2}}+\sqrt{S_{3}})^{2}.
Поскольку
S_{1}=\frac{l^{2}(\ctg\alpha+\ctg\beta)}{2}=\frac{l^{2}\sin(\alpha+\beta)}{2\sin\alpha\sin\beta}=\frac{l^{2}\sin(180^{\circ}-\gamma)}{2\sin\alpha\sin\beta}=\frac{l^{2}\sin\gamma}{2\sin\alpha\sin\beta}=\frac{l^{2}\sin^{2}\gamma}{2\sin\alpha\sin\beta\sin\gamma},
S_{2}=\frac{m^{2}\sin\alpha}{2\sin\gamma\sin\beta}=\frac{m^{2}\sin^{2}\alpha}{2\sin\gamma\sin\beta\sin\alpha},~S_{3}=\frac{n^{2}\sin\beta}{2\sin\alpha\sin\gamma}=\frac{n^{2}\sin\beta}{2\sin\alpha\sin\gamma\sin\beta},
то
S_{\triangle ABC}=(\sqrt{S_{1}}+\sqrt{S_{2}}+\sqrt{S_{3}})^{2}=\frac{(l\sin\gamma+m\sin\alpha+n\sin\beta)^{2}}{2\sin\alpha\sin\beta\sin\gamma}.
Источник: Вступительный экзамен на химический факультет МГУ. — 1979, вариант 2, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 43
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 7.28, с. 54
