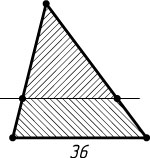
3054. Основание треугольника равно 36. Прямая, параллельная основанию, делит площадь треугольника пополам. Найдите длину отрезка этой прямой, заключённого между сторонами треугольника.
Ответ. 18\sqrt{2}
.
Указание. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Решение. Указанная прямая отсекает от данного треугольника подобный ему треугольник, площадь которого относится к площади данного как 1:2
. Поэтому коэффициент подобия равен \frac{1}{\sqrt{2}}
. Следовательно, длина искомого отрезка равна \frac{1}{\sqrt{2}}\cdot36=18\sqrt{2}
.
Источник: Делоне Б. Н., Житомирский О. К. Задачник по геометрии. — М.—Л.: ОГИЗ, 1949. — № 198, с. 20
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.068, с. 163
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 7.6, с. 52
