3060. Медианы треугольника равны 3, 4 и 5. Найдите площадь треугольника.
Ответ. 8.
Указание. Докажите, что площадь треугольника, образованного медианами данного треугольника, составляет \frac{3}{4}
площади данного треугольника.
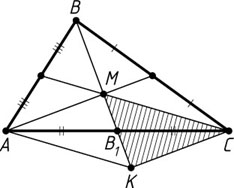
Решение. Пусть B_{1}
— середина стороны AC
треугольника ABC
, M
— точка пересечения его медиан. На продолжении медианы BB_{1}
за точку B_{1}
отложим отрезок B_{1}K
, равный MB_{1}
. Тогда AMCK
— параллелограмм, CK=AM
.
Стороны треугольника KMC
составляют \frac{2}{3}
соответствующих медиан треугольника ABC
. Поэтому треугольник KMC
подобен с коэффициентом \frac{2}{3}
треугольнику, стороны которого равны медианам треугольника ABC
. Тогда площадь треугольника KMC
составляет \frac{4}{9}
площади треугольника со сторонами 3, 4, 5, т. е. \frac{4}{9}\cdot6=\frac{8}{3}
. Следовательно,
S_{\triangle ABC}=6S_{\triangle B_{1}MC}=6\cdot\frac{1}{2}S_{\triangle KMC}=8.
