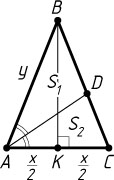
3064. В равнобедренном треугольнике ABC
(AB=BC
) проведена биссектриса AD
. Площади треугольников ABD
и ADC
равны соответственно S_{1}
и S_{2}
. Найдите AC
.
Ответ. \frac{2\sqrt{S_{2}(S_{1}+S_{2})}}{\sqrt[{4}]{{4S_{1}^{2}-S_{2}^{2}}}}
.
Указание. Обозначьте AB=BC=y
, AC=x
и составьте систему из двух уравнений.
Решение. Обозначим AB=BC=y
, AC=x
. Пусть BK
— высота треугольника ABC
. Тогда
S_{2}+S_{1}=\frac{1}{2}AC\cdot BK=\frac{1}{2}x\sqrt{y^{2}-\frac{x^{2}}{4}},
\frac{S_{1}}{S_{2}}=\frac{BD}{DC}=\frac{AB}{AC}=\frac{y}{x}.
Выразим y
из второго уравнения и подставим в первое. После возведения обеих частей в квадрат получим:
\frac{x^{4}(4S^{2}_{1}-S^{2}_{2})}{4S^{2}_{2}}=4(S_{1}+S_{2})^{2}.
Отсюда находим, что
x=\frac{2\sqrt{S_{2}(S_{1}+S_{2})}}{\sqrt[{4}]{{4S_{1}^{2}-S_{2}^{2}}}}.
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 119, с. 17
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 119, с. 15
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 7.25, с. 54
