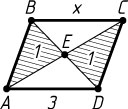
3070. Диагонали выпуклого четырёхугольника ABCD
пересекаются в точке E
. Известно, что площадь каждого из треугольников ABE
и DCE
равна 1, площадь всего четырёхугольника не превосходит 4, AD=3
. Найдите сторону BC
.
Ответ. 3.
Указание. Докажите, что BC\parallel AD
.
Решение. Треугольники ABD
и ACD
равновелики, так как
S_{\triangle ABD}=S_{\triangle ABE}+S_{\triangle AED}=S_{\triangle DCE}+S_{\triangle AED}=S_{\triangle ACD}.
Тогда их высоты, опущенные на общее основание AD
, равны. Следовательно, BC\parallel AD
.
Пусть BC=x
. Из подобия треугольников BEC
и DEA
следует, что
\frac{BE}{ED}=\frac{BC}{AD}=\frac{x}{3},
поэтому
S_{\triangle BEC}=\frac{BE}{ED}\cdot S_{\triangle DCE}=\frac{x}{3},
S_{\triangle DEA}=\frac{DE}{BE}\cdot S_{\triangle ABE}=\frac{3}{x}.
По условию задачи S_{ABCD}\leqslant4
, поэтому
\frac{x}{3}+\frac{3}{x}\leqslant2.
С другой стороны, сумма двух взаимно обратных положительных чисел не меньше 2, причём равенство достигается тогда и только тогда, когда каждое из этих чисел равно 1.
\frac{x}{3}+\frac{3}{x}=2,~\frac{x}{3}=\frac{3}{x}=1,~x=3.
Источник: Вступительный экзамен на экономический факультет МГУ. — 1985, вариант 1, № 6
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 138
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 7.26, с. 54
Источник: Всесибирская физико-математическая олимпиада. — 2016, заключительный этап, задача 5, 8 класс
