3083. Площадь трапеции ABCD
равна S
, отношение оснований \frac{AD}{BC}=3
. На прямой, пересекающей продолжение основания AD
за точку D
, расположен отрезок EF
, причём AE\parallel DF
, BE\parallel CF
и \frac{AE}{DF}=\frac{CF}{BE}=2
. Найдите площадь треугольника EFD
(найдите все решения).
Ответ. \frac{1}{4}S
, \frac{9}{20}S
.
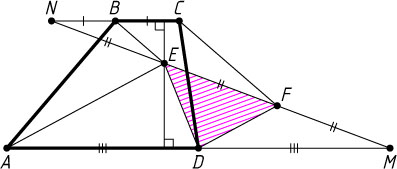
Указание. Пусть точка N
— точка пересечения прямых EF
и BC
. Тогда либо B
— середина NC
, либо N
лежит на отрезке DC
и \frac{BN}{NC}=\frac{1}{2}
.
Решение. Пусть M
— точка пересечения прямых EF
и AD
. Поскольку точка D
лежит между точками A
и M
, то из условия задачи следует, что D
— середина отрезка AM
.
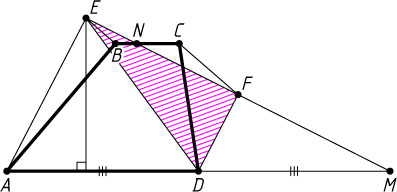
Пусть N
— точка пересечения прямых EF
и BC
. Возможны два её положения: либо B
— середина отрезка NC
(рис. 1), либо N
лежит на отрезке BC
и \frac{BN}{NC}=\frac{1}{2}
(рис. 2). Обозначим BC=a
. Тогда AD=DM=3a
.
В первом случае NE=EF=FM
. Поэтому, если провести высоту трапеции через точку E
, то она разделится этой точкой в отношении \frac{1}{2}
.
Пусть h
— высота трапеции. Тогда \frac{2}{3}h
— высота треугольника AEM
, поэтому
S_{\triangle AEM}=\frac{1}{2}AM\cdot\frac{2}{3}h=3a\cdot\frac{2}{3}h=2ah,
а так как S=\frac{1}{2}(3a+a)h=2ah
, то
S_{\triangle AEM}=S,~S_{\triangle EDF}=\frac{1}{4}S.
Во втором случае EF=FM
, EN=\frac{1}{2}FN
. Поэтому высота треугольника DEM
, опущенная из вершины E
, равна \frac{6}{5}h
,
S_{\triangle DEM}=\frac{1}{2}\cdot3a\cdot\frac{6}{5}h=\frac{9}{5}ah=\frac{9}{10}S,
S_{\triangle EFD}=\frac{1}{2}S_{\triangle DEM}=\frac{9}{20}S.
Источник: Вступительный экзамен в МФТИ. — 1975, билет 1, № 5
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 75-1-5, с. 177
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 214, с. 25

