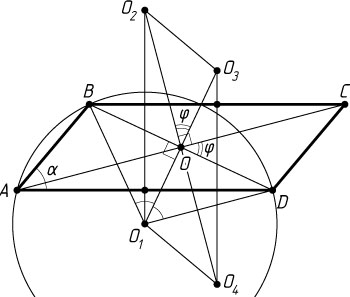
3087. В параллелограмме ABCD
острый угол BAD
равен \alpha
. Пусть O_{1}
, O_{2}
, O_{3}
, O_{4}
— центры окружностей, описанных соответственно около треугольников DAB
, DAC
, DBC
, ABC
. Найдите отношение площади четырёхугольника O_{1}O_{2}O_{3}O_{4}
к площади параллелограмма ABCD
.
Ответ. \ctg^{2}\alpha
.
Указание. Проведите четыре серединных перпендикуляра к сторонам параллелограмма. Их пересечение образует параллелограмм O_{1}O_{2}O_{3}O_{4}
.
Решение. Рассмотрим четырёхугольник, вершины которого — точки пересечения четырёх серединных перпендикуляров к сторонам данного параллелограмма. Это также параллелограмм, и его вершины — это точки O_{1}
, O_{2}
, O_{3}
и O_{4}
. Обозначим через O
общий центр этих параллелограммов.
Пусть острый угол между диагоналями параллелограмма ABCD
равен \varphi
. Тогда острый угол между диагоналями параллелограмма O_{1}O_{2}O_{3}O_{4}
также равен \varphi
(острые углы с соответственно перпендикулярными сторонами равны).
Рассмотрим окружность с центром O_{1}
, описанную около треугольника ABD
. Центральный угол BO_{1}D
вдвое больше вписанного угла BAD
, поэтому
\angle BO_{1}O=\frac{1}{2}\angle BO_{1}D=\angle BAD=\alpha.
Из прямоугольного треугольника BO_{1}O
находим, что \frac{OO_{1}}{BO}=\ctg\alpha
. Аналогично находим, что \frac{OO_{2}}{AO}=\ctg\alpha
. Следовательно,
\frac{S_{O_{1}O_{2}O_{3}O_{4}}}{S_{ABCD}}=\frac{\frac{1}{2}O_{1}O_{3}\cdot O_{2}O_{4}\sin\varphi}{\frac{1}{2}BD\cdot AC\sin\varphi}=
=\frac{O_{1}O_{3}}{BD}\cdot\frac{O_{2}O_{4}}{AC}=\frac{O_{1}O}{BO}\cdot\frac{OO_{2}}{AO}=\ctg\alpha\cdot\ctg\alpha=\ctg^{2}\alpha.
Источник: Вступительный экзамен в МФТИ. — 1975, билет 5, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 75-5-3, с. 179
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.36, с. 89
