3093. На сторонах AB
, AC
и BC
правильного треугольника ABC
расположены соответственно точки C_{1}
, B_{1}
и A_{1}
так, что треугольник A_{1}B_{1}C_{1}
— правильный. Отрезок BB_{1}
пересекает сторону C_{1}A_{1}
в точке O
, причём \frac{BO}{OB_{1}}=k
. Найдите отношение площади треугольника ABC
к площади треугольника A_{1}B_{1}C_{1}
.
Ответ. 1+3k
.
Указание. Найдите отношение перпендикуляров, опущенных из точек B
и B_{1}
на прямую A_{1}C_{1}
.
Решение. Если Q
— точка пересечения отрезков CC_{1}
и A_{1}B_{1}
, то
\frac{CQ}{QB_{1}}=\frac{BO}{OB_{1}}=k.
Аналогично для точки пересечения отрезков AA_{1}
и B_{1}C_{1}
.
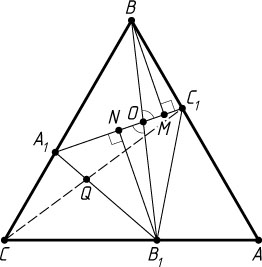
Опустим из точек B
и B_{1}
перпендикуляры BM
и B_{1}N
на прямую A_{1}C_{1}
. Тогда треугольники BMO
и B_{1}NO
подобны,
\frac{BM}{B_{1}N}=\frac{BO}{OB_{1}}=k.
Поэтому S_{\triangle A_{1}C_{1}B}=kS_{\triangle A_{1}B_{1}C_{1}}
. Аналогично получим равенства:
S_{\triangle B_{1}C_{1}A}=kS_{\triangle A_{1}B_{1}C_{1}},~S_{\triangle A_{1}B_{1}C}=kS_{\triangle A_{1}B_{1}C_{1}}.
Значит,
S_{\triangle ABC}=S_{\triangle A_{1}B_{1}C_{1}}+3kS_{\triangle A_{1}B_{1}C_{1}}=(1+3k)S_{\triangle A_{1}B_{1}C_{1}}.
Следовательно,
\frac{S_{\triangle ABC}}{S_{\triangle A_{1}B_{1}C_{1}}}=3k+1.
Источник: Вступительный экзамен в МФТИ. — 1972, билет 5, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 72-5-4, с. 154
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 7.31, с. 55
