3100. Через точку K
, данную на стороне AB
треугольника ABC
, проведите прямую так, чтобы она разделила площадь треугольника пополам.
Решение. Если точка K
совпадает с серединой P
стороны AB
, то искомая прямая — это прямая CP
, так как медиана треугольника делит его на два равновеликих треугольника.
Пусть точка K
не совпадает с P
. Через точку P
проведём прямую, параллельную CK
. Если K
лежит между точками A
и P
, то проведённая прямая пересекает сторону BC
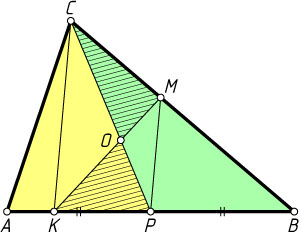
. Пусть M
— точка пересечения, O
— точка пересечения диагоналей CP
и KM
трапеции CKPM
. Тогда
S_{\triangle OKP}=S_{\triangle OCM},~S_{\triangle BCP}=\frac{1}{2}S_{\triangle ABC},
поэтому
S_{\triangle BKM}=S_{BPOM}+S_{\triangle OKP}=S_{BPOM}+S_{\triangle OCM}=S_{\triangle BPC}=\frac{1}{2}S_{\triangle ABC}.
Следовательно, прямая KM
делит треугольник ABC
на две равновеликие части.
Если K
лежит между точками B
и P
, то прямая, проведённая через точку P
параллельно CK
, пересекает сторону AC
. Остальное аналогично.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 38, с. 81
Источник: Вступительный экзамен в МФТИ. — 1954, билет 1, № 1
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 54-1-1, с. 47
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 25, с. 208
Источник: Готман Э. Г. Задачи по планиметрии и методы их решения. — М.: Просвещение, 1996. — № 372, с. 108
