3110. В треугольнике ABC
, площадь которого равна 6, на стороне AB
взята точка K
, делящая эту сторону в отношении AK:BK=2:3
, а на стороне AC
взята точка L
, делящая AC
в отношении AL:LC=5:3
. Точка Q
пересечения прямых CK
и BL
расположена на расстоянии 1,5 от прямой AB
. Найдите сторону AB
.
Ответ. 4.
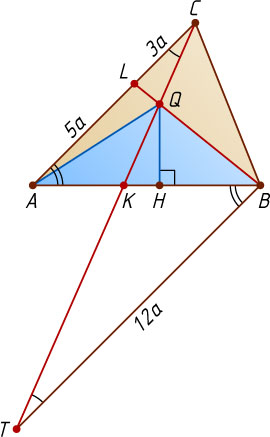
Решение. Первый способ. Положим AL=5a
, LC=3a
. Тогда AC=8a
. Через точку B
проведём прямую, параллельную AC
и продолжим отрезок CK
до пересечения с этой прямой в точке T
. Из подобия треугольников BKT
и AKC
находим, что
BT=\frac{BK}{AK}\cdot AC=\frac{3}{2}\cdot8a=12a,
а из подобия треугольников BQT
и LQC
—
\frac{BQ}{QL}=\frac{BT}{LC}=\frac{12a}{3a}=4,
поэтому \frac{BQ}{BL}=\frac{4}{5}
.
У треугольников ABL
и ABC
одна и та же высота, проведённая из вершины B
, значит, отношение их площадей равно отношению оснований, т. е. \frac{S_{\triangle ABL}}{S_{\triangle ABC}}=\frac{AL}{AC}=\frac{5}{8}
. Аналогично, \frac{S_{\triangle ABQ}}{S_{\triangle ABL}}=\frac{BQ}{BL}=\frac{4}{5}
. Следовательно,
S_{\triangle ABQ}=\frac{4}{5}S_{\triangle ABL}=\frac{4}{5}\cdot\frac{5}{8}S_{\triangle ABC}=\frac{4}{5}\cdot\frac{5}{8}\cdot6=3.
Пусть QH
— высота треугольника ABQ
. Тогда
S_{\triangle ABQ}=\frac{1}{2}AB\cdot QH=\frac{1}{2}AB\cdot\frac{3}{2}=\frac{3}{4}AB=3.
Отсюда находим, что AB=4
.
Второй способ. Отношение площадей треугольников AQC
и BQC
с общим основанием CQ
равно отношению высот, опущенных на это основание. В свою очередь, отношение этих высот равно отношению AK:BK=2:3
. Значит, S_{\triangle AQC}=\frac{2}{3}S_{\triangle BQC}
. Аналогично, S_{\triangle AQB}=\frac{5}{3}S_{\triangle BQC}
. Тогда
6=S_{\triangle AQB}+S_{\triangle BQC}+S_{\triangle AQC}=\frac{5}{3}S_{\triangle BQC}+S_{\triangle BQC}+\frac{2}{3}S_{\triangle BQC}=\frac{10}{3}S_{\triangle BQC}
находим, что S_{\triangle BQC}=\frac{9}{5}
. Следовательно,
S_{\triangle AQB}=\frac{5}{3}S_{\triangle BQC}=\frac{5}{3}\cdot\frac{9}{5}=3.
Пусть QH
— высота треугольника ABQ
. Тогда
S_{\triangle ABQ}=\frac{1}{2}AB\cdot QH=\frac{1}{2}AB\cdot\frac{3}{2}=\frac{3}{4}AB=3.
Отсюда находим, что AB=4
.
Источник: Вступительный экзамен на геологический факультет МГУ. — 1978 (отделение геофизики), вариант 2, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 78
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 6.14, с. 47
