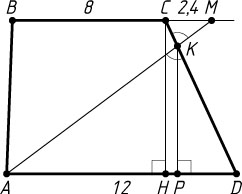
3114. В трапеции ABCD
даны основания AD=12
и BC=8
. На продолжении стороны BC
выбрана такая точка M
, что CM=2{,}4
. В каком отношении прямая AM
делит площадь трапеции ABCD
?
Ответ. 1:1
.
Решение. Пусть отрезки AM
и CD
пересекаются в точке K
. Из подобия треугольников MKC
и AKD
находим, что
\frac{CK}{KD}=\frac{CM}{AD}=\frac{2{,}4}{12}=\frac{1}{5}.
Опустим перпендикуляры KP
и CH
на AD
. Из подобия прямоугольных треугольников KPD
и CHD
следует, что
\frac{KP}{CH}=\frac{KD}{CD}=\frac{5}{6},
поэтому KP=\frac{5}{6}CH
. Значит.
S_{ABCD}=\frac{BC+AD}{2}\cdot CH=\frac{8+12}{2}\cdot CH=10CH,
S_{\triangle AKD}=\frac{1}{2}AD\cdot KP=\frac{1}{2}\cdot12\cdot\frac{5}{6}CH=5CH.
Следовательно,
\frac{S_{\triangle AKD}}{S_{ABCD}}=\frac{1}{2},~\frac{S_{\triangle AKD}}{S_{ABCK}}=1.
Источник: Вступительный экзамен на экономический факультет МГУ. — 1979 (отделение политической экономии), вариант 2, № 2C
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 14.12, с. 112
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 107
