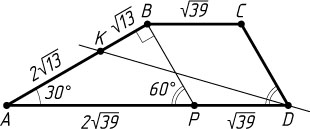
3138. Дана трапеция ABCD
с основаниями AD=3\sqrt{39}
и BC=\sqrt{39}
. Кроме того дано, что угол BAD
равен 30^{\circ}
, а угол ADC
равен 60^{\circ}
. Через точку D
проходит прямая, делящая трапецию на две равновеликие фигуры. Найдите длину отрезка этой прямой, находящегося внутри трапеции.
Ответ. 13.
Указание. Указанная прямая пересекает отрезок AB
. Пусть K
— точка пересечения. Найдите отношение высот треугольника AKD
и трапеции.
Решение. Поскольку S_{\triangle ABD}=3S_{\triangle BCD}
, то указанная прямая пересекает отрезок AB
. Пусть K
— точка пересечения. Тогда
S_{\triangle AKD}=\frac{1}{2}S_{ABCD}=\frac{1}{2}\cdot\frac{AD+BC}{2}h=h\sqrt{39},
где h
— высота трапеции ABCD
. С другой стороны,
S_{\triangle AKD}=\frac{1}{2}AD\cdot h_{1}=\frac{3\sqrt{39}\cdot h_{1}}{2},
где h_{1}
— высота треугольника AKD
. Поэтому \frac{h_{1}}{h}=\frac{2}{3}
и \frac{AK}{AB}=\frac{2}{3}
.
Проведём через вершину B
прямую, параллельную стороне CD
, до пересечения с основанием AD
в точке P
. Тогда
AP=AD-DP=AD-BC=2\sqrt{39}.
Из прямоугольного треугольника ABP
находим, что
AB=AP\cos30^{\circ}=3\sqrt{13}.
Поэтому AK=\frac{2}{3}AB=2\sqrt{13}
. По теореме косинусов из треугольника AKD
находим:
DK^{2}=AK^{2}+AD^{2}-2AK\cdot AD\cos30^{\circ}=
=4\cdot13+9\cdot39-2\cdot2\sqrt{13}\cdot3\sqrt{39}\cdot\frac{\sqrt{3}}{2}=169.
Следовательно, DK=13
.
Источник: Вступительный экзамен на геологический факультет МГУ. — 1968, вариант 2, № 2
Источник: Моденов П. С. Экзаменационные задачи по математике с анализом их решения. — М.: Просвещение, 1969. — вариант 2, № 2, с. 332
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.26, с. 31
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 4, с. 138
