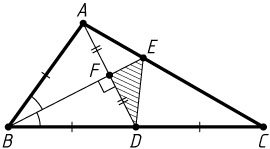
3152. В треугольнике ABC
медиана AD
и биссектриса BE
перпендикулярны и пересекаются в точке F
. Известно, что площадь треугольника DEF
равна 5. Найдите площадь треугольника ABC
.
Ответ. 60.
Указание. Треугольник ABD
— равнобедренный.
Решение. Треугольник ABD
— равнобедренный, так как его биссектриса BF
является высотой. Поэтому
AF=FD~\Rightarrow~S_{\triangle AFE}=S_{\triangle DFE}=5.
Кроме того, BC=2BD=2AB
. Тогда по свойству биссектрисы треугольника
\frac{EC}{AE}=\frac{BC}{AB}=2.
Следовательно,
S_{\triangle DEC}=2S_{\triangle ADE}=4S_{\triangle DEF}=20,~S_{\triangle ADC}=30.
Значит,
S_{\triangle ABC}=2S_{\triangle ADC}=60.
Источник: Вступительный экзамен на географический факультет МГУ. — 1992, вариант 2, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 609
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 7, с. 5
