3153. В треугольнике ABC
биссектриса BE
и медиана AD
перпендикулярны и имеют одинаковую длину, равную 4. Найдите стороны треугольника ABC
.
Ответ. \sqrt{13}
, 2\sqrt{13}
, 3\sqrt{5}
.
Указание. Треугольник ABD
— равнобедренный.
Решение. Пусть P
— точка пересечения отрезков BE
и AD
. Треугольник ABD
— равнобедренный, так как его биссектриса BP
является высотой. Поэтому
AP=PD=2,~BC=2BD=2AB.
По свойству биссектрисы треугольника
\frac{CE}{AE}=\frac{BC}{AB}=2,~\mbox{т. е.}~AC=3AE.
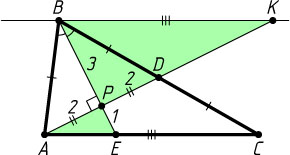
Проведём через вершину B
прямую, параллельную AC
. Пусть K
— точка пересечения этой прямой с продолжением медианы AD
. Тогда BK=AC=3AE
.
Из подобия треугольников APE
и KPB
следует, что
\frac{PE}{BP}=\frac{AE}{BK}=\frac{1}{3}.
Поэтому PE=1
и BP=3
. Следовательно,
AB=\sqrt{AP^{2}+BP^{2}}=\sqrt{13},~BC=2AB=2\sqrt{13},
AE=\sqrt{AP^{2}+EP^{2}}=\sqrt{5},~AC=3AE=3\sqrt{5}.
Источник: Вступительный экзамен на географический факультет МГУ. — 1992, № 4, вариант 1
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 2.24.1, с. 22
