3159. Через точку, взятую на диагонали AC
параллелограмма ABCD
, проведены прямые, параллельные его сторонам. Данный параллелограмм делится таким образом на четыре параллелограмма, из которых два имеют своими диагоналями части диагонали AC
. Докажите, что два других параллелограмма равновелики.
Указание. Рассмотрите образовавшиеся подобные треугольники и воспользуйтесь формулой площади параллелограмма: S=ab\sin\alpha
.
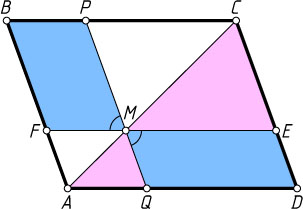
Решение. Пусть M
— точка на диагонали AC
параллелограмма ABCD
; прямая, проходящая через точку M
параллельно AB
, пересекает стороны BC
и AD
в точках P
и Q
соответственно, а прямая, проходящая через точку M
параллельно BC
, пересекает стороны AB
и CD
в точках F
и E
соответственно. Тогда из подобия треугольников CME
и MAQ
следует, что
\frac{CE}{ME}=\frac{MQ}{AQ},~CE\cdot AQ=ME\cdot MQ.
Поэтому
S_{MQDE}=MQ\cdot ME\sin\angle EMQ=CE\cdot AQ\sin\angle EMQ=
=MP\cdot MF\sin\angle FMP=S_{MPBF}.
