3165. Диагональ трапеции делит её площадь в отношении 3:7
. В каком отношении разделится площадь этой трапеции, если из конца меньшего основания провести прямую, параллельную боковой стороне?
Ответ. 3:2
.
Указание. Площади треугольников с соответственно равными основаниями относятся как их высоты.
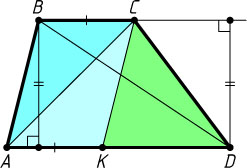
Решение. Пусть BC
— меньшее основание трапеции ABCD
и \frac{S_{\triangle BCD}}{S_{\triangle ABD}}=\frac{3}{7}
. Высоты треугольников BCD
и ABD
, опущенные соответственно из вершин D
и B
, равны высоте данной трапеции. Следовательно,
\frac{BC}{AD}=\frac{S_{\triangle BCD}}{S_{\triangle ABD}}=\frac{3}{7}.
Пусть K
— точка точка на основании AD
, что CK\parallel AB
. Тогда
AK=BC,~KD=AD-AK=AD-BC.
Поэтому \frac{AK}{KD}=\frac{3}{4}
. Следовательно,
\frac{S_{ABCK}}{S_{\triangle CKD}}=2\cdot\frac{S_{\triangle ACK}}{S_{\triangle CKD}}=2\cdot\frac{AK}{KD}=\frac{6}{4}=\frac{3}{2}.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 114, с. 89
