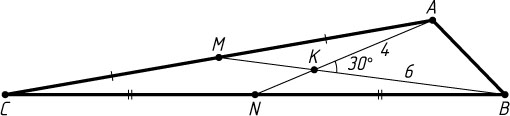
3170. Медианы AN
и BM
треугольника ABC
равны 6 и 9 соответственно и пересекаются в точке K
, причём угол AKB
равен 30^{\circ}
. Найдите площадь треугольника ABC
.
Ответ. 18.
Указание. Медианы треугольника делятся их точкой пересечения в отношении 2:1
, считая от вершины.
Решение. Поскольку медианы делятся их точкой пересечения в отношении 2:1
, считая от вершины треугольника, то
AK=\frac{2}{3}AN=4,~BK=\frac{2}{3}BM=6.
Поэтому
S_{\triangle AKB}=\frac{1}{2}BK\cdot AK\sin\angle AKB=6.
Следовательно,
S_{\triangle ABC}=3S_{\triangle AKB}=18.
Источник: Вступительный экзамен в МАТИ. — 1988, № 5, вариант 2
Источник: Журнал «Квант». — 1989, № 5, с. 71
