3174. Пусть AA_{1}
и BB_{1}
— высоты остроугольного неравнобедренного треугольника ABC
. Известно, что отрезок A_{1}B_{1}
пересекает среднюю линию, параллельную AB
, в точке C'
. Докажите, что отрезок CC'
перпендикулярен прямой, проходящей через точку пересечения высот и центр описанной окружности треугольника ABC
.
Решение. Пусть M
и N
— середины сторон соответственно AC
и BC
треугольника ABC
, H
— точка пересечения высот, O
— центр описанной окружности. Предположим, что BC\gt AC
.
Поскольку AA_{1}
и BB_{1}
— высоты треугольника, а MN
— средняя линия,
\angle A_{1}B_{1}M=\angle ABC=\angle A_{1}NM,
значит, точки A_{1}
, B_{1}
, M
и N
лежат на одной окружности. Обозначим её \omega_{1}
.
Из точек A_{1}
и B_{1}
отрезок CH
виден под прямым углом, значит, эти точки лежат на окружности с диаметром CH
. Обозначим её \omega_{2}
.
Из точек M
и N
отрезок CO
виден под прямым углом, значит, эти точки лежат на окружности с диаметром CO
. Обозначим её \omega_{3}
.
Отрезок A_{1}B_{1}
— общая хорда окружностей \omega_{1}
и \omega_{2}
, отрезок MN
— общая хорда окружностей \omega_{1}
и \omega_{3}
. Эти отрезки пересекаются в точке C'
, следовательно, общая хорда CK
окружностей \omega_{2}
и \omega_{3}
также проходит через точку C'
.
Пусть P
и Q
— середины отрезков CH
и CO
. Тогда P
— центр окружности \omega_{2}
, а Q
— центр окружности \omega_{3}
. Отрезок PQ
перпендикулярен общей хорде CK
этих окружностей, а так как PQ
— средняя линия треугольника COH
, то CK\perp OH
. Что и требовалось доказать.
Аналогично для случая, когда BC\lt AC
.
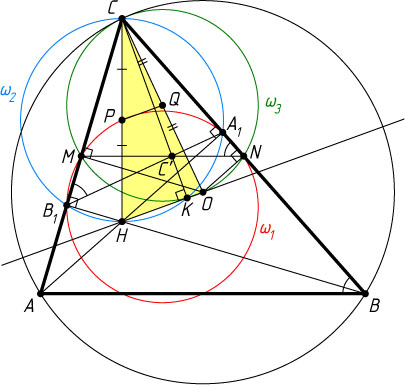
Автор: Емельянов Л. А.
Источник: Всероссийская олимпиада школьников. — 2004-05, XXXI, окружной этап, 11 класс
Источник: Агаханов Н. Х. и др. Всероссийские математические олимпиады школьников. 1993—2006. — М.: МЦНМО, 2007. — № 388, с. 51
