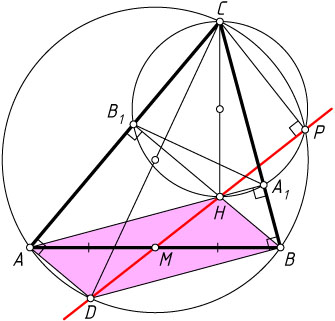
3180. Высоты AA_{1}
и BB_{1}
остроугольного треугольника ABC
пересекаются в точке H
. Описанные окружности треугольников ABC
и A_{1}B_{1}C
вторично пересекаются в точке P
. Докажите, что прямая PH
проходит через середину отрезка AB
.
Указание. Пусть прямая PH
вторично пересекает описанную окружность треугольника ABC
в точке D
. Тогда BD
— диаметр этой окружности, а четырёхугольник AHCD
— параллелограмм.
Решение. Из точек A_{1}
и B_{1}
отрезок CH
виден под прямым углом, значит, эти точки лежат на окружности с диаметром CH
. Поэтому описанная окружность треугольника A_{1}B_{1}C
проходит через точку H
.
Пусть прямая PH
вторично пересекает описанную окружность треугольника ABC
в точке D
. Тогда CD
— диаметр этой окружности (так как \angle CPD=\angle CPH=90^{\circ}
), поэтому \angle CAD=\angle CBD=90^{\circ}
.
Прямые AD
и DH
параллельны, так как они перпендикулярны одной и той же прямой AC
. Аналогично BD\parallel AH
, значит, четырёхугольник AHBD
— параллелограмм. Его диагональ DH
проходит через середину M
диагонали AB
. Отсюда следует доказываемое утверждение.
Примечание. 1. Это утверждение верно и для тупоугольного неравнобедренного треугольника.
2. См. статью Ю.Блинкова «Ортоцентр, середина стороны, точка пересечения касательных и ... ещё одна точка!», Квант, 2014, N1, с.43-46.
Источник: Журнал «Квант». — 2012, № 5-6, с. 59; 2014, № 1, с. 43
