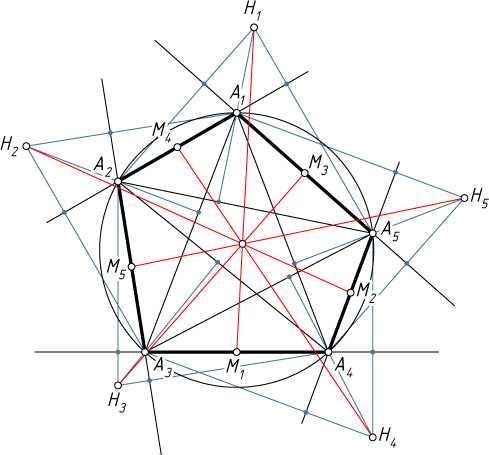
3184. Пусть A_{1}A_{2}A_{3}A_{4}A_{5}
— вписанный выпуклый пятиугольник, H_{1}
— ортоцентр треугольника A_{2}A_{1}A_{5}
, M_{1}
— середина стороны A_{3}A_{4}
, l_{1}
— прямая, проходящая через точки H_{1}
и M_{1}
. Аналогично определяются прямые l_{2}
, l_{3}
, l_{4}
и l_{5}
. Докажите что все эти прямые l_{i}
пересекаются в одной точке.
Указание. Пусть H_{2}
— ортоцентр треугольника A_{3}A_{2}A_{1}
, M_{2}
— середина стороны A_{4}A_{5}
. Тогда отрезки M_{1}M_{2}
и H_{2}M_{2}
пересекаются и делятся точкой пересечения в отношении 1:2
, считая от точек M_{1}
и M_{2}
.
Решение. Лемма 1. Пусть H
— точка пересечения высот треугольника ABC
, O
— центр описанной окружности. Тогда \overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}
.
Доказательство. Рассмотрим сумму векторов \overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OK}
. Отрезок OK
— диагональ ромба OAKB
. Поэтому OK\perp AB
. Следовательно, OK\parallel CH
. Тогда, если \overrightarrow{OK}+\overrightarrow{OC}=\overrightarrow{OM}
, то точка M
принадлежит высоте, проходящей через вершину C
.
Таким образом, если \overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OH'}
, то точка H'
принадлежит каждой высоте треугольника ABC
. Следовательно, точки H'
и H
совпадают. Лемма доказана.
Лемма 2. Четырёхугольник ABCD
вписанный. Пусть H_{c}
и H_{b}
— ортоцентры треугольников ABD
и ACD
соответственно. Тогда четырёхугольник BCH_{b}H_{c}
— параллелограмм.
Доказательство. Применяя лемму 1 к треугольникам ABD
и ACD
, получим, что
\overrightarrow{H_{c}H_{b}}=\overrightarrow{OH_{b}}-\overrightarrow{OH_{c}}=(\overrightarrow{OA}+\overrightarrow{OC}+\overrightarrow{OD})-(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OD})=\overrightarrow{OC}-\overrightarrow{OB}=\overrightarrow{BC}.
Значит, H_{c}H_{b}\parallel BC
и H_{c}H_{b}=BC
. Следовательно, BCH_{b}H_{c}
— параллелограмм. Лемма доказана.
Перейдём к нашей задаче. Пусть H_{2}
— ортоцентр треугольника A_{3}A_{2}A_{1}
, M_{2}
— середина стороны A_{4}A_{5}
, l_{2}
— прямая, проходящая через точки H_{2}
и M_{2}
.
Из леммы леммы 2 следует, что H_{1}H_{2}\parallel A_{3}A_{5}
и H_{1}H_{2}=A_{3}A_{5}
, а так как M_{1}M_{2}
— средняя линия треугольника A_{3}A_{4}A_{5}
, то M_{1}M_{2}\parallel A_{3}A_{5}
и M_{1}M_{2}=\frac{1}{2}A_{3}A_{5}
. Поэтому M_{1}M_{2}\parallel H_{1}H_{2}
и M_{1}M_{2}=\frac{1}{2}H_{1}H_{2}
. Значит, отрезки H_{1}M_{1}
и H_{2}M_{2}
пересекаются и делятся точкой пересечения в отношении 1:2
, считая от точек M_{1}
и M_{2}
. Аналогично для любой пары соответствующих отрезков. Следовательно, все прямые l_{i}
проходят через одну точку. Что и требовалось доказать.
Источник: Журнал «Квант». — 2012, № 5-6, с. 59
