3195. Пусть E
, F
, G
— такие точки на сторонах соответственно AB
, BC
, CA
треугольника ABC
, для которых \frac{AE}{EB}=\frac{BF}{FC}=\frac{CG}{GA}=k
, где 0\lt k\lt1
. Найдите отношение площади треугольника, образованного прямыми AF
, BG
и CE
, к площади треугольника ABC
.
Ответ. \frac{(1-k)^{3}}{1-k^{3}}
.
Указание. Найдите отношение, в котором делятся точкой пересечения отрезки CE
и BG
.
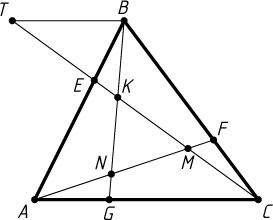
Решение. Пусть K
— точка пересечения отрезков CE
и BG
. Через точку B
проведём прямую, параллельную AC
, и продолжим CE
до пересечения с этой прямой в точке T
. Треугольники BET
и AEC
подобны с коэффициентом \frac{1}{k}
. Поэтому
BT=\frac{1}{k}AC=\frac{1}{k}\cdot\frac{1+k}{k}CG=\frac{1+k}{k^{2}}CG.
Из подобия треугольников BKT
и GKC
находим, что
\frac{BK}{KG}=\frac{BT}{CG}=\frac{1+k}{k^{2}}.
Поэтому
S_{\triangle CGK}=\frac{KG}{BG}S_{\triangle CBG}=\frac{k^{2}}{1+k+k^{2}}S_{\triangle CBG}=
=\frac{k^{2}}{1+k+k^{2}}\cdot\frac{k}{k+1}S_{\triangle ABC}=\frac{k^{3}}{(k+1)(1+k+k^{2})}S_{\triangle ABC}.
Аналогично находим, что
S_{\triangle AME}=S_{\triangle BNF}=\frac{k^{3}}{(k+1)(1+k+k^{2})}S_{\triangle ABC},
где M
— точка пересечения AF
и CE
, а N
— AF
и BG
. Следовательно,
S_{\triangle MNK}=S_{\triangle ABC}-S_{\triangle ABF}-S_{\triangle BCK}-S_{\triangle ACE}+S_{\triangle AME}+S_{\triangle BNF}+S_{\triangle CKG}=
=S_{\triangle ABC}-\frac{3k}{k+1}S_{\triangle ABC}+\frac{3k^{3}}{(k+1)(1+k+k^{2})}S_{\triangle ABC}=
=\left(1-\frac{3k}{k+1}+\frac{3k^{3}}{(k+1)(1+k+k^{2})}\right)S_{\triangle ABC}=
=\left(1-\frac{3k(k+1)}{(k+1)(1+k+k^{2})}\right)S_{\triangle ABC}=\left(1-\frac{3k}{1+k+k^{2}}\right)S_{\triangle ABC}=
=\frac{(1-k)^{2}}{1+k+k^{2}}S_{\triangle ABC}=\frac{(1-k)^{3}}{1-k^{3}}S_{\triangle ABC}.
Значит,
\frac{S_{\triangle MNK}}{S_{\triangle ABC}}=\frac{(1-k)^{3}}{1-k^{3}}.
Автор: Сойфер А. Л.
Источник: Польские математические олимпиады. — 1950, задача 5
Источник: Страшевич С., Бровкин Е. Польские математические олимпиады. — М.: Мир, 1978. — № 17, с. 13
Источник: Журнал «Квант». — 1971, № 1, с. 39, М65(a)
Источник: Задачник «Кванта». — М65(а)
