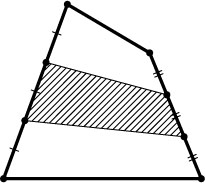
3205. Два непересекающихся отрезка делят каждую из двух противоположных сторон выпуклого четырёхугольника на три равные части (см.рис.). Докажите, что между этими прямыми заключена треть площади четырёхугольника.
Указание. Пусть точки M
и N
лежат на стороне AB
выпуклого четырёхугольника ABCD
, точки K
и L
— на стороне DC
, причём
AM=MN=NB,~DL=LK=KC.
Проведите диагонали DM
, LN
и KB
четырёхугольников AMLD
, MNKL
и NBCK
. Тогда высота треугольника LMN
, проведённая из вершины L
, есть среднее арифметическое высот треугольников DAM
и KBN
, проведённых из вершин K
и D
.
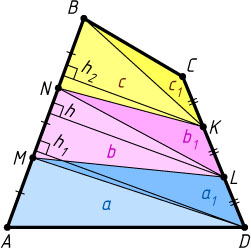
Решение. Пусть точки M
и N
лежат на стороне AB
выпуклого четырёхугольника ABCD
, точки K
и L
— на стороне DC
, причём
AM=MN=NB,~DL=LK=KC.
Проведём диагонали DM
, LN
и KB
четырёхугольников AMLD
, MNKL
и NBCK
. Обозначим
S_{\triangle AMD}=a,~S_{\triangle DLM}=a_{1},~S_{\triangle MNL}=b,~S_{\triangle KLN}=b_{1},~S_{\triangle NBK}=c,~S_{\triangle CKB}=c_{1}.
Пусть h_{1}
, h
и h_{2}
— расстояния от точек соответственно D
, L
и K
до прямой AB
. Тогда
h=\frac{h_{1}+h_{2}}{2},~a=\frac{1}{2}AM\cdot h_{1},~b=\frac{1}{2}MN\cdot h,~c=\frac{1}{2}NB\cdot h_{2}.
Следовательно, b=\frac{a+c}{2}
.
Аналогично b_{1}=\frac{a_{1}+c_{1}}{2}
. Поэтому
b+b_{1}=\frac{a+c}{2}+\frac{a_{1}+c_{1}}{2}=\frac{(a+a_{1})+(c+c_{1})}{2},
или
S_{MNKL}=\frac{S_{AMLD}+S_{NBCK}}{2}.
Следовательно, S_{MNKL}=\frac{1}{3}S_{ABCD}
.
Источник: Васильев Н. Б. и др. Заочные математические олимпиады. — Л.—М.: Наука, 1981. — № 3-3, с. 45
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 12.9, с. 93