3207. Разделим каждую сторону выпуклого четырёхугольника ABCD
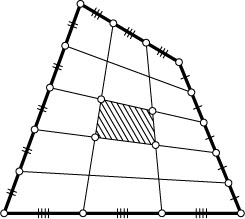
на три равные части и соединим отрезками соответствующие точки на противоположных сторонах (см.рис.). Докажите, что площадь «среднего» четырёхугольника в 9 раз меньше площади четырёхугольника ABCD
.
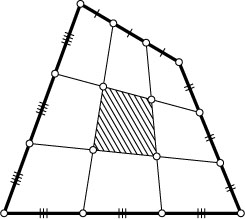
Указание. Докажите что указанные отрезки делят друг друга на три равные части.
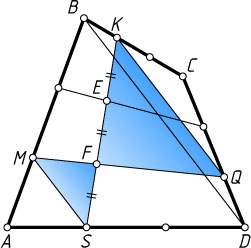
Решение. Докажем сначала, что указанные отрезки делят друг друга на три равные части. Обозначим точки деления, как показано на рис. 1, и соединим точки M
и S
, K
и Q
.
Из подобия треугольников MAS
и BAD
следует, что SM\parallel BD
и \frac{SM}{BD}=\frac{1}{3}
, а из подобия треугольников KCQ
и BCD
— KQ\parallel BD
и \frac{KQ}{BD}=\frac{2}{3}
. Поэтому SM\parallel KQ
и \frac{SM}{KQ}=\frac{1}{2}
. Следовательно, треугольники MFS
и QFK
подобны с коэффициентом \frac{1}{2}
. Значит, \frac{SF}{FK}=\frac{1}{2}
. Аналогично докажем, что \frac{EK}{SE}=\frac{1}{2}
. Следовательно,
SF=FE=EK.
Аналогично для остальных отрезков.
Теперь докажем, что площадь четырёхугольника MNPQ
составляет третью часть площади четырёхугольника ABCD
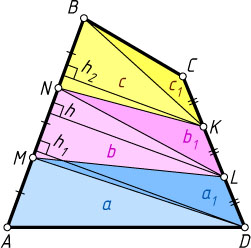
. Соединим точки, как показано на рис. 2, и обозначим площади образовавшихся треугольников через a
, a_{1}
, b
, b_{1}
, c
, c_{1}
. Пусть h_{1}
, h
и h_{2}
— расстояния от точек D
, Q
и P
до прямой AB
. Тогда
h=\frac{h_{1}+h_{2}}{2},~a=\frac{1}{2}AM\cdot h_{1},~b=\frac{1}{2}MN\cdot h,~c=\frac{1}{2}NB\cdot h_{2},~b=\frac{a+c}{2}.
Аналогично b_{1}=\frac{a_{1}+c_{1}}{2}
. Поэтому
b+b_{1}=\frac{a+c}{2}+\frac{a_{1}+c_{1}}{2}=\frac{(a+a_{1})+(c+c_{1})}{2},
или
S_{MNPQ}=\frac{S_{AMQD}+S_{NBCP}}{2}.
Следовательно, S_{MNPQ}=\frac{1}{3}S_{ABCD}
. Таким образом, по доказанному
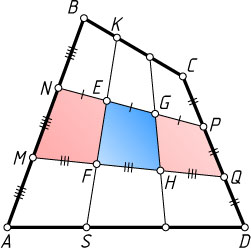
S_{FEGH}=\frac{1}{3}S_{MNPQ}=\frac{1}{9}S_{ABCD}
(рис. 3).
Примечание. Верно более общее утверждение. Если стороны AB
и CD
выпуклого четырёхугольника ABCD
разделены на m
, а стороны BC
и AD
— на n
равных частей (m
и n
нечётны), то площадь «центрального» четырёхугольника в mn
раз меньше площади четырёхугольника ABCD
.
Автор: Лопшиц А. М.
Источник: Журнал «Квант». — 1976, № 1, с. 50, М362
Источник: Задачник «Кванта». — М362




