3208. Три прямые, параллельные сторонам треугольника ABC
и проходящие через одну точку, отсекают от треугольника ABC
трапеции. Три диагонали этих трапеций, не имеющие общих концов, делят треугольник на семь частей, из которых четыре — треугольники. Докажите, что сумма площадей трёх из этих треугольников, прилегающих к сторонам треугольника ABC
, равна площади четвёртого.
Указание. Указанные диагонали трапеций отсекают от треугольника ABC
три треугольника, сумма площадей которых равна площади треугольника ABC
.
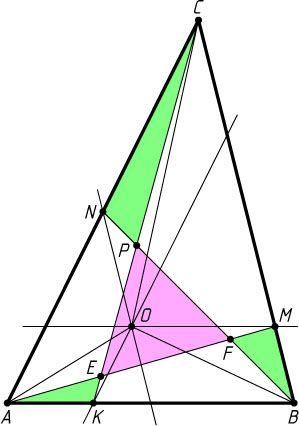
Решение. Пусть O
— точка внутри треугольника ABC
, через которую проведены три прямые; AM
, BN
, CK
— указанные диагонали трёх трапеций.
Поскольку OM\parallel AB
, то S_{\triangle ABM}=S_{\triangle ABO}
. Аналогично
S_{\triangle BCN}=S_{\triangle BCO},~S_{\triangle ACK}=S_{\triangle ACO}.
Поэтому
S_{\triangle ABM}+S_{\triangle BCN}+S_{\triangle ACK}=S_{\triangle ABO}+S_{\triangle BCO}+S_{\triangle ACO}=S_{\triangle ABC}.
Если EFP
— «внутренний» треугольник, то
S_{\triangle EFP}=S_{\triangle ABC}-S_{\triangle ABM}-S_{\triangle BCN}-S_{\triangle ACK}+
+S_{\triangle AKE}+S_{\triangle BMF}+S_{\triangle CPN}=
=S_{\triangle ABC}-S_{\triangle ABC}+S_{\triangle AKE}+S_{\triangle BMF}+S_{\triangle CPN}=
=S_{\triangle AKE}+S_{\triangle BMF}+S_{\triangle CPN}.
Автор: Косьянчук В.
Источник: Журнал «Квант». — 1978, № 11, с. 18, М534
Источник: Задачник «Кванта». — М534
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 4.33, с. 86
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 4.34, с. 85
