3214. Из середины каждой стороны остроугольного треугольника опущены перпендикуляры на две другие стороны. Докажите, что площадь ограниченного этими перпендикулярами шестиугольника равна половине площади треугольника.
Указание. Разбейте указанный шестиугольник на четыре треугольника средними линиями данного треугольника.
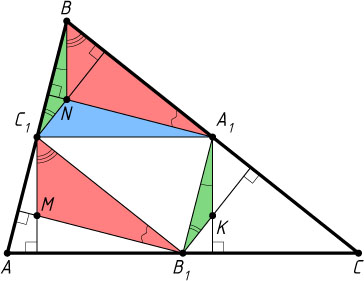
Решение. Пусть A_{1}
, B_{1}
, C_{1}
— середины сторон соответственно BC
, AC
, AB
остроугольного треугольника ABC
; пусть также перпендикуляры, опущенные из точки C_{1}
на AC
и из точки B_{1}
на AB
, пересекаются в точке M
; из точки C_{1}
на BC
и из точки A_{1}
на AB
— в точке N
; из точки A_{1}
на AC
и из точки B_{1}
на BC
— в точке K
. Тогда M
, N
, K
— точки пересечения высот треугольников AB_{1}C_{1}
, BA_{1}C_{1}
, CA_{1}B_{1}
соответственно.
Треугольник C_{1}MB_{1}
равен треугольнику BNA_{1}
, а треугольник A_{1}KB_{1}
— треугольнику BNC_{1}
(по стороне и двум прилежащим к ней углам). Следовательно,
S_{A_{1}KB_{1}MC_{1}N}=S_{\triangle A_{1}B_{1}C_{1}}+S_{\triangle A_{1}NC_{1}}+S_{\triangle C_{1}MB_{1}}+S_{\triangle A_{1}KB_{1}}=
=S_{\triangle A_{1}B_{1}C_{1}}+S_{\triangle A_{1}NC_{1}}+S_{\triangle BNA_{1}}+S_{\triangle BNC_{1}}=
=S_{\triangle A_{1}B_{1}C_{1}}+S_{\triangle A_{1}BC_{1}}=\frac{1}{4}S_{\triangle ABC}+\frac{1}{4}S_{\triangle ABC}=\frac{1}{2}S_{\triangle ABC}.
Автор: Азамов А. А.
Источник: Всесоюзная олимпиада по математике. — 1985, XIX, 8 класс
Источник: Журнал «Квант». — 1985, № 4, с. 36, М916
Источник: Задачник «Кванта». — М916
Источник: Васильев Н. Б., Егоров А. А. Задачи всесоюзных математических олимпиад. — М.: Наука, 1988. — № 395, с. 93
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 4.62, с. 88
Источник: Всероссийская олимпиада школьников. — 2016-2017, XLIII, школьный этап, 11 класс
Источник: Журнал «Crux Mathematicorum». — 2007, № 5, задача 4, с. 290
Источник: Немецкие математические олимпиады. — 2003
