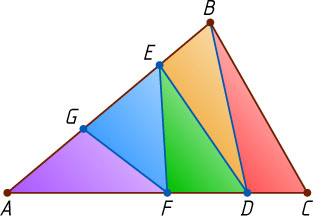
3218. Как в треугольнике ABC
провести ломаную BDEFG
(см. рис.), чтобы все пять полученных треугольников имели одинаковые площади?
Указание. Если M
— точка на стороне BC
треугольника ABC
, то \frac{S_{\triangle BAM}}{S_{\triangle CAM}}=\frac{BM}{CM}
.
Решение. Поскольку S_{\triangle BDC}=\frac{1}{5}S_{\triangle ABC}
, то CD=\frac{1}{5}AC
. Тогда
S_{\triangle BDE}=\frac{1}{5}S_{\triangle ABC}=\frac{1}{5}\cdot\frac{5}{4}S_{\triangle ABD}=\frac{1}{4}S_{\triangle ABD},
поэтому BE=\frac{1}{4}AB
. Аналогично DF=\frac{1}{3}AD
и AG=\frac{1}{2}AE
.
