3219. Отрезки AK
, BM
, CN
и DL
делят квадрат ABCD
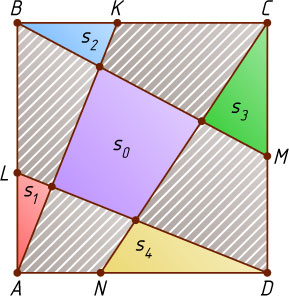
со стороной 1 на четыре треугольника с площадями s_{1}
, s_{2}
, s_{3}
, s_{4}
и пять четырёхугольников (см.рис.). Площадь центрального четырёхугольника равна s_{0}
, причём s_{0}=s_{1}+s_{2}+s_{3}+s_{4}
. Докажите равенство:
AL+BK+CM+DN=2.
Указание. Докажите, что
S_{\triangle ABK}+S_{\triangle BCM}+S_{\triangle CDN}+S_{\triangle DAL}=S_{ABCD}.
Решение. Поскольку
s_{0}=S_{ABCD}-S_{\triangle ABK}-S_{\triangle BCM}-S_{\triangle CDN}-S_{\triangle DAL}+s_{1}+s_{2}+s_{3}+s_{4},~s_{0}=s_{1}+s_{2}+s_{3}+s_{4},
то
S_{\triangle ABK}+S_{\triangle BCM}+S_{\triangle CDN}+S_{\triangle DAL}=S_{ABCD},
или
\frac{1}{2}BK\cdot AB+\frac{1}{2}CM\cdot BC+\frac{1}{2}DN\cdot CD+\frac{1}{2}AL\cdot AD=AB\cdot BC,
а так как AB=BC=CD=AD=1
, то
\frac{1}{2}(BK+CM+DN+AL)=1,~\mbox{или}~BK+CM+DN+AL=2.
Примечание. Это утверждение верно для любого ромба.
Автор: Сефибеков С. Р.
Источник: Журнал «Квант». — 1992, № 3, с. 18, М1331
Источник: Задачник «Кванта». — М1331
