3220. Через точку X
, лежащую внутри параллелограмма, проведены прямые, параллельные его сторонам. Докажите, что два образовавшихся при этом параллелограмма с единственной общей вершиной X
равновелики тогда и только тогда, когда точка X
лежит на диагонали параллелограмма.
Указание. Пусть точка X
лежит внутри параллелограмма ABCD
. Если S_{ABCX}=S_{ADCX}
, то точка X
лежит на диагонали AC
.
Решение. Пусть точка X
лежит внутри параллелограмма ABCD
, прямая, проведённая через эту точку параллельно стороне AB
, пересекает стороны BC
и AD
соответственно в точках P
и Q
, а прямая, проведённая через эту точку параллельно стороне BC
, пересекает стороны AB
и CD
соответственно в точках R
и S
. Тогда четырёхугольники ARXQ
, XPCS
, RBPX
и QXSD
— параллелограммы.
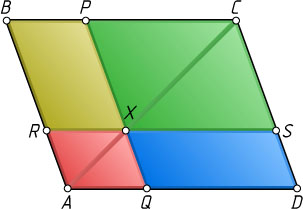
Если точка X
лежит на диагонали AC
(рис. 1), то
S_{\triangle ABC}=S_{\triangle ADC},~S_{\triangle ARX}=S_{\triangle AQX},~S_{\triangle XPC}=S_{\triangle XSC}.
Следовательно,
S_{RBPX}=S_{\triangle ABC}-S_{\triangle ARX}-S_{\triangle XPC}=S_{\triangle ADC}-S_{\triangle AQX}-S_{\triangle XSC}=S_{QXSD},
что и требовалось доказать.
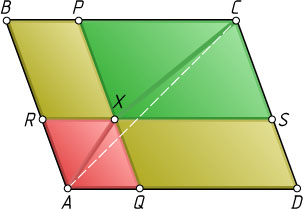
Обратно, пусть точка X
лежит внутри параллелограмма ABCD
и S_{RBPX}=S_{QXSD}
(рис. 2). Поскольку
S_{\triangle ARX}=S_{\triangle AQX}~\mbox{и}~S_{\triangle XPC}=S_{\triangle XSC},
то
S_{ABCX}=S_{\triangle ARX}+S_{\triangle XPC}+S_{RBPX}=S_{\triangle AQX}+S_{\triangle XSC}+S_{QXSD}=S_{ADCX}=\frac{1}{2}S_{ABCD}=S_{\triangle ABC}.
Следовательно, точка X
лежит на диагонали AC
.
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 4.19, с. 83

